[알고리즘] CH01. Analyzing Algorithms and Problems
Analyzing Algorithms and Problems : Principles and Examples
◼️ 알고리즘이란?
➞ 문제를 해결하는 잘 정의된 절차
◼️ Example - Unordered Array(정렬되지 않은 배열)에서의 Search
◻️ Problem)
• E를 n개의 엔트리, E[0], …, E[n-1]을 포함하는 배열
• 배열에 K가 있는 경우, 지정된 키 K의 인덱스를 찾음
• K가 배열에 없는 경우, –1을 답으로 반환합니다.
◻️ Strategy)
• 일치하는 항목이 발견되거나 배열이 모두 사용될 때까지 K를 각 항목과 차례로 비교
• K가 배열에 없으면 답으로 -1을 반환
◻️ Algorithm)
• Input : E, n, K, 여기서 E, n, K, 여기서 E는 n개의 항목(인덱스 0, …, n-1)을 가진 배열이고, K는 찾는 항목
단순화를 위해, K와 E의 엔트리가 n과 같이 정수라고 가정
• Output : 배열 E의 K의 위치를 답으로 return (K를 찾을 수 없는 경우 -1 return)
• Step :
int seqSearch(int[] E, int n, int K)
1. int ans, index;
2. ans = -1; // K를 찾을 수 없는 경우 -1 return
3. for (index = 0; index < n; index++)
4. if (K == E[index])
5. ans = index; // E의 K의 위치 return
6. break;
7. return ans;알고리즘 표현 방법
1) 슈도코드
2) 순서도( Flow Chart )
◻️ Analysis of the Algorithm (알고리즘의 분석)
이 예제에서의
▪️ Basic Operation
➝ 배열의 원소와 비교
▪️ Worst case 분석
여기서 worst case란, Basic operations이 가장 많은 케이스
➝ K가 배열의 마지막 위치에 있는 경우
➝ K가 배열에 존재하지 않는 경우
이 예제에서는 W(n) = n
◻️ More Analysis of the Algorithm
▪️ Average-Behavior Analysis
- 가정이 필요
- 확률 필요
- 랜덤성 필요
위의 이유들로, Worst Case보다 어려움
▪️ Optimality
▪️ Correctness
◻️ Analysis Tool : Mathematics

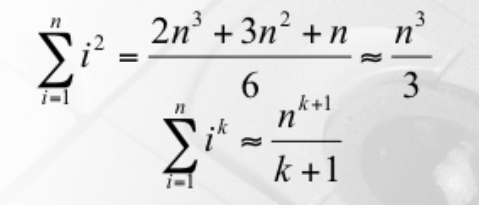

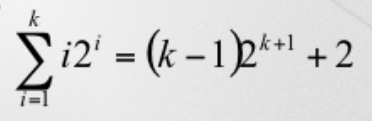
◻️ Analysis Tool : Logic
